Constructive Precedence Relationships

Hemlock’s parser implementation relies on the hocc parser generator, which spiritually descends from the Parsing parser generator. In most respects both hocc and Parsing merely synthesize best practices for LR(1) parsing, with the important exception that they provide an unusually precise conflict resolution mechanism. Parsing validated the approach, but viewed through the lens of, “If it’s hard to explain, it’s hard to use”, a compelling refinement emerged for hocc. Read on for details.

Precedence precedent

In the dark ages preceding the invention of LR(1) parsing, there was a more limited approach called precedence parsing. Long ago, no later than the advent of Yacc, practitioners integrated precedence as a conflict resolution mechanism for LR-family (e.g. LALR) parser generators. Conflict resolution enables compact grammar specifications that would otherwise have to be hierarchically decomposed.

The following example from the yacc manual demonstrates how operator precedence can disambiguate the parse tree for e.g. a = b = c*d - e - f*g as equivalent to a = (b = (((c*d) - e) - (f*g))). Note that operators are declared in increasing precedence order, so = is of lowest precedence in the example.

%right '='
%left '+' '-'
%left '*' '/'

%%

expr : expr '=' expr
     | expr '+' expr
     | expr '-' expr
     | expr '*' expr
     | expr '/' expr
     | NAME
     ;

This works well for many grammars, but the status quo is a hair-trigger footgun, viz:

• A total ordering is induced on all operators, even for operator pairs that are mutually irrelevant. This can cause unintentional implicit conflict resolution that hides grammar flaws.
• Each production’s precedence defaults to that of its rightmost token. In combination with the total ordering for operator precedence, this is especially problematic for productions like:

  expr : expr '+' expr
       | '(' expr '+' expr')'
       ;
  

  The default can be overridden, but without extreme care unintentional implicit conflict resolution can hide grammar flaws.

  expr : expr '+' expr
       | '(' expr '+' expr')' %prec '+'
       ;
  

A better approach

Solutions to the problems described above are conceptually straightforward:

• Make precedence relationships explicit rather than implicit, so that it is possible to express the absence of precedence ordering.
• Allow arbitrary directed acyclic precedence graphs (DAGs), so that e.g. x and y in a < x < b and a < y < b have no ordering relationship.
• By default assign each production a unique disjoint precedence, so that conflict resolution never occurs implicitly.

Aside from some tangential associativity enhancements, this is how Parsing and hocc improve conflict resolution. But there’s one Parsing implementation gotcha that almost survived in hocc. It was possible to express <, =, and > precedence relationships, which could induce cycles. Parsing dealt with this by generating a Graphviz dot representation of the precedence relationship graph, so that if there was a cycle in the graph, Parsing could generate a fatal error and the programmer could scrutinize the graph. But experience showed that understanding and resolving cycles was a mind-warping, difficult aspect of parser implementation. Consider Lyken’s [¹] precedence graph, and imagine figuring out a fix when accidentally introducing a cycle:

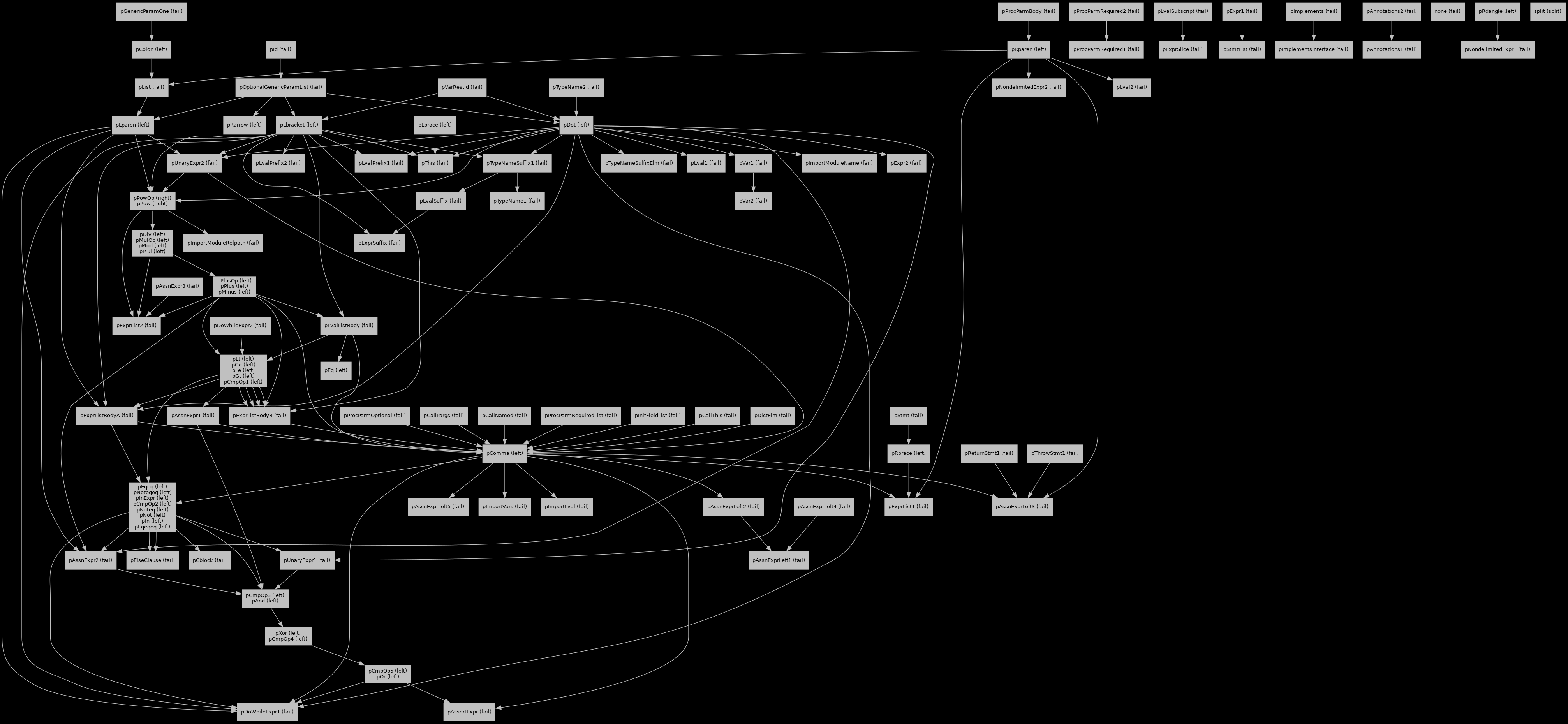Lyken’s precedence graph (link to readable version)

Parsing extracts grammar grammar specifications from Python docstrings, which among other things means that the developer doesn’t necessarily have full control over specification statement ordering. But hocc implements a stand-alone specification language, so there’s no compelling reason to allow syntax that could express cycles. Earlier designs of hocc supported syntax like the following:

hocc
    prec p2 <p1
    prec p1
    prec p3 <p1
    prec p4 <[p2; p3] =p5 >p1
    prec p5

Yep, there’s a cycle in there. hocc now restricts specification syntax/semantics to enforce a valid linearization of the induced DAG:

• Require that each precedence is declared before it is referenced.
• Remove the = and > relationships so that it is impossible to “tie the knot” and create a cycle.

Absent the cycle, the above example is now restricted to a form equivalent to the following:

hocc
    prec p1
    prec p2 < p1
    prec p3 < p1
    prec p4 < p2, p3

This forced linearization approximates the visual representation of the DAG to a degree that there is no practical need for an actual visual. The temptation was strong to mimic DAG rendering in the most excellent tig tool for git repositories, but hocc doesn’t need such sophistication. Mark this one down as another instance of working hard to avoid problems, rather than endlessly working to solve hard problems.

Footnotes

1. Lyken was an uncompleted programming language that incubated jemalloc and Parsing. ↩