Natural Numerical Tower Foundations

Hemlock is a systems programming language that has to be capable of integration with languages like C and Fortran. More generally, Hemlock needs to be capable of utilizing the various numerical representations for which the computer provides native implementations. For integers that means at least signed/unsigned 8/16/32/64-bit integers. Hemlock uses a uniform naming scheme for these: u8, u16, u32, u64 (aka uns), i8, i16, i32, and i64 (aka int). But Hemlock doesn’t stop there because there are various practical uses for wider integers. For example the built-in hashing currently uses u128, and will use u256 once we convert from MurmurHash3 to BLAKE3. We chose to support through u512/i512 in service of e.g. SHA3-512, leaving the door open for even wider integers as practical need arises. However, no matter how wide we go with fixed-width integer types, there are situations in which we need even more precision for intermediate computations. This is where the nat and zint types come in.

All of Hemlock’s fixed-width integer types have well-defined modular arithmetic semantics, which means that their number lines wrap around. For example, if we decrement 0u8, the result is 255u8. This is of course not the case for the nat (ℕ₀) and zint (ℤ) types, which have infinite bounds. The only danger zone is nat subtraction. For example, Nat.pred 0n halts, because the result is outside the domain of ℕ₀.

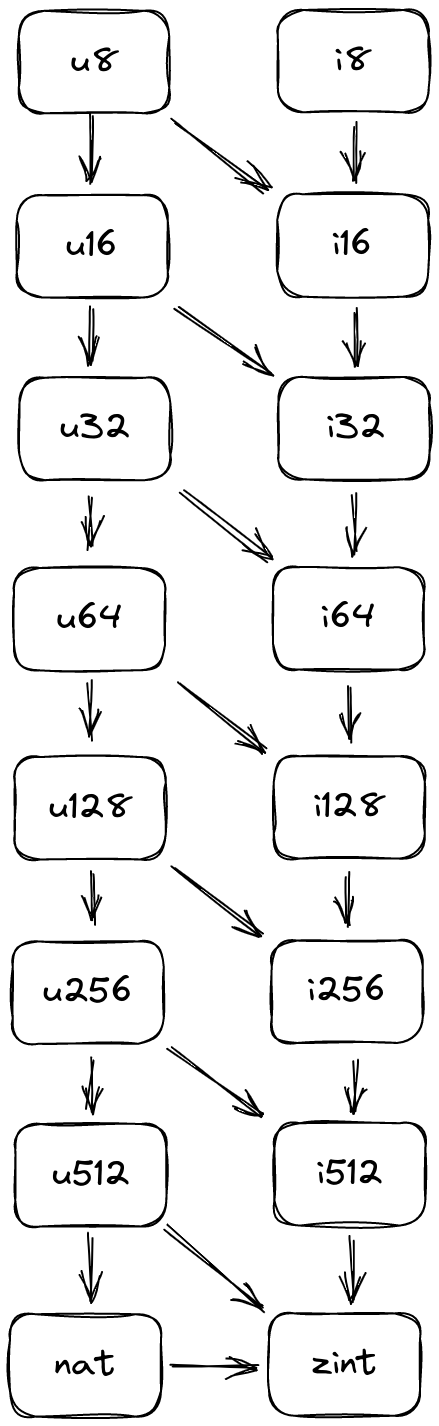
The nat and zint types provide a, shall we say, natural foundation for Hemlock’s integer numerical tower. The Scheme language has a magnificent numerical tower for which integers are only the top of the tower, but similar concepts apply to Hemlock’s integers. u8 values can always be exactly converted to wider unsigned types, but the converse is not true. Things get a bit trickier in the context of signedness. u8 cannot necessarily be exactly converted to i8, but i16 and wider work fine. And i8 cannot necessarily be exactly converted to any unsigned type. The resulting numerical tower has a consistent, if surprising structure. Every source/target pair for paths through the directed graph corresponds to total conversion from the source type to the target type; any other conversion is partial and may fail.

An easier way to only get correct answers

Let’s go back to the claim that we always need more precision than the widest fixed-width integer type. Suppose we only had u8 in Hemlock and our compiler was incrementally computing the value of 235 while scanning the digits. These incremental computations would conceptually look something like the following happy case.

open U8
u = 2u8               # Scan '2' -> 2
u' = u * 10u8 + 3u8   # Scan '3' -> 23
u'' = u' * 10u8 + 5u8 # Scan '5' -> 235

All is well and good, but suppose the input is 267 (multiplication would wrap) or 257 (addition would wrap). Now we have to check every intermediate result for wrapping in order to detect an out-of-range input! The control flow and multiplication overflow detection are finicky enough that I’m not going to bother showing any details here; just use your imagination to replace every * and + with a chain of functions that do tricky overflow detection. Now contrast that with a nat-based approach.

open Nat
u = 2n              # Scan '2' -> 2
u' = u * 10n + 3n   # Scan '3' -> 23
u'' = u' * 10n + 5n # Scan '5' -> 235
result_opt = U8.narrow_of_nat_opt u''

Ah, blissful simplicity — all the overflow detection happens in one place! This same general approach works well in a variety of contexts. Take a problem similar to the Nat.pred 0n example above.

# Imagine `n0` and `n1` are dynamically computed.
n0 = 0n
n1 = 1n
z = Zint.((Nat.bits_to_zint n0) - (Nat.bits_to_zint n1))
result_opt = Nat.like_of_zint_opt z

zint serves as a nexus type here, whereas nat was sufficient for the earlier example. Depending on context, even fixed-width types may serve as a nexus type, though care is required when choosing. For example, a single u64 multiplication can use u128 as the nexus type, but even two multiplications may overflow u128.

As shown earlier, this isn’t the only way to deal with overflow, but it’s an awful lot easier to work with in practice. Hemlock pays the one-time complexity cost of implementing nat and zint, and reaps the innumerable simplification benefits in Hemlock application code.